ratio (logFC) 以外に発現変動遺伝子を判定する方法として用いられるものに、 Z-score があります。あまり聞きなれない用語かもしれませんが、偏差値というとどうでしょうか?
ある値が、その群の平均値から、標準偏差 (SD) の何個ぶん離れているかを求めたものが、 Z-score です。Z-score の考え方自体は、特殊なものではありません。Z-検定 (Z-test) という使われ方もあります。(Z-score 化されるのは、logFC に限りません。例えば、 cBioPortal では、シグナル値が Z-score 化されています。)
ここで用いるのは、 logFC を Z-score 化したものです。ある logFC が、 logFC の平均値から、標準偏差の何個ぶん離れているか計算します。
ratio (logFC) のヒストグラム
ratio (logFC) のヒストグラムを示します。データは、解析例1のものを使っています。
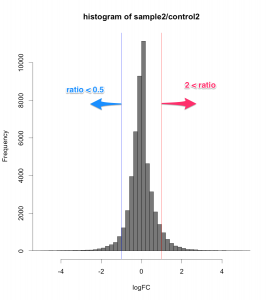
ほとんどの遺伝子の logFC が0(つまりratio=1)、変動していないことが分かるかと思います。ratio で判定するなら、 ratio > 2 または、 ratio < 0.5 を満たす部分に含まれる遺伝子を発現変動遺伝子と判定していることになります。(ヒストグラムの右側と左側)。
標準偏差と Z-score
次に、同じヒストグラムに標準偏差 (SD) と Z-score の関係を示してみます。
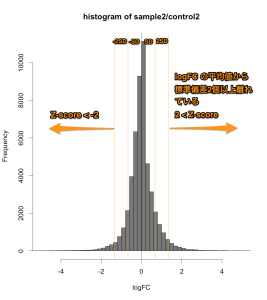
解析例1のデータ (sample2/control2) の場合、計算してみると、logFC の平均値は、ほぼ0になります。SDは、約 0.672 です。また、分布関数の考え方から、平均値から標準偏差2個分離れていれば、稀な値 (p-value < 0.05) ということになります。
したがって、 Z-score で判定する場合は、下記のようになります。
- 増加した遺伝子: Z-score > 2
- 減少した遺伝子: Z-score < -2
絶対値の記号を用いれば、両方を合わせて、 |Z-score| > 2 とも書けます。
追記:2SDだと、2 x 0.672 = 1.344 なので、 logFC > 1.344 であれば、 Z-score > 2 です。ratio で言い換えると、ratio > 2.54 であれば、Z-score > 2 となります。
参考
